Выбор числа элементов памяти и кодирование состояний автомата
Пред.Страница След.Страница Раздел Содержание
3. Выбор числа элементов памяти и кодирование состояний автомата. Кодирование состояний заключается в том, что каждому состоянию si
О S однозначным образом ставится в соответствие набор внутренних переменных у1, у2, ..., уh. Состояния и соответствующие им коды обычно представляют в виде таблицы, которая называется таблицей кодирования состояний автомата.
Если автомат имеет l состояний, то, для того, чтобы получить однозначное соответствие, необходимо иметь не менее l различных двоичных кодов. Последнее условие можно записать в виде l Ј 2h. Откуда находим
] log2l [ Ј
h, (1)
где ] a [ означает ближайшее целое, не меньшее а.
Из неравенства (1) следует, что минимальное число элементов памяти, необходимое для получения однозначного кодирования,
h = ] log2 l [.
Кодирование состояний существенно влияет на сложность комбинационной части схемы автомата. Для того, чтобы упростить комбинационную схему, часто используют избыточное кодирование, выбирая h большим, чем это необходимо для получения однозначного кодирования. Избыточное кодирование используется также для построения схем без состязаний. Кодирование состояний кажется целесообразным выполнять совместно с кодированием входных и выходных сигналов, однако такая задача оказывается весьма сложной и практически не реализуется.
4. Построение функций возбуждения.Функция возбуждения yi' определяет, какой сигнал нужно подать на вход i-го элемента памяти, чтобы получить код состояния, в которое автомат должен перейти. Функции возбуждения при структурном синтезе соответствуют функциям перехода абстрактного автомата. Это соответствие показывает, что функции возбуждения должны зависеть от внутренних переменных y1, y2, ..., yh, определяющих состояние автомата, и входных переменных х1, х2, ..., хn, относящихся к одному и тому же моменту времени. Последнее обстоятельство позволяет нам рассматривать функции возбуждения как
переключательные функции:
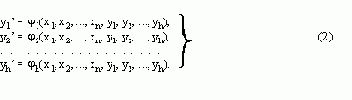
Пред.Страница След.Страница Раздел Содержание
