Кодирование с числом элементов памяти, равным числу состояний
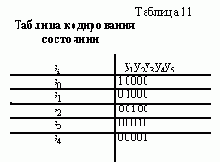
Этот способ кодирования заключается в том, что каждому из l состояний автомата ставится в соответствие один элемент памяти. В каждый момент времени только один элемент памяти должен находиться в состоянии “1”, а остальные - в состоянии “0”, поскольку автомат может находиться только в одном состоянии. Пример кодирования пяти состояний описанным способом приведен в табл. 11. Используемый способ часто называют кодированием с применением кодов “один из l”. Следует отметить, что этот способ кодирования позволяет упростить процедуру построения функций возбуждения и функций выходов за счет исключения этапа минимизации. Остановимся на этом вопросе подробнее.
Если для кодирования состояний используются l двоичных переменных у1, y2
, ..., yl, то существует 2l
различных двоичных наборов значений этих переменных. Обозначим множество всех двоичных наборов Н. Разобьем это множество на l пересекающихся подмножеств H1, H2, ..., Hl
таким образом, чтобы в каждое подмножество Hl входили 2l-1 двоичных наборов, определяющих переключательную функцию вида yi. В каждое подмножество Hi
входит только один набор ~xi, используемый при кодировании. Он состоит из l - 1 нуля и одной единицы, стоящей на i-м месте. При этом множество Hi ' = Hi - ~xi, представляет собой совокупность неиспользованных двоичных наборов.
Пусть автомат переходит из состояния s', которому приписан код ~xi , в состояние s”, которому приписан код ~xi, под действием набора входных сигналов d1, d2, ...,dn. Если в качестве элемента памяти используется триггер D, то функция возбуждения, реализующая такой переход , имеет вид :
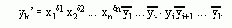
Представим эту функцию следующим образом: yk' = x1d1 x2d2
... xndnc(у1, y2, ..., yl). Функция c(у1, y2, ..., yl). является неполностью определенной переключательной функцией. Доопределим ее единицами на всех наборах, входящих в множество Hi'. В результате получаем функцию, совокупность единичных наборов которой совпадает с множеством Hi. Согласно построению, такая функция является переменной yi, поэтому имеем yk' = x1d1 x2d2
... xndn уi
Приведенные рассуждения показывают, что при выбранном способе кодирования каждый дизъюнктивный член функций возбуждения (функций выхода) содержит только одну внутреннюю переменную, определяющую соответствующее состояние автомата. Пред.Страница След.Страница Раздел Содержание
