Гонками
элементов памяти. При этом говорят, что состязание выигрывает элемент, обладаюший наименьшей задержкой.
Состязания элементов памяти приводят к тому, что автомат при зменении состояния не сразу оказывается в том состоянии, которое запланировано условиями работы, а переходит в него через несколько нпредусмотренных транзитных состояний. В результате такого перехода, независимо от соотношений задержек элементов памяти, авомат достигает того состояния, в которое он должен перейти, то состязания называются
некритическими. Если же существует жотя бы одно сочетание значений задержек элементов памяти, при котором автомат не достигает запланированного состояния, то состязания называются критическими.
Рассмотрим, как происходят состязания на примерах, используя таблицу переходов, приведенную на рис. 3. В клетках таблицы, соответствующих сходным состояниям, находятся кружки с цыфрой. Каждая цыфра является номером рассматриваемого примера. Точками в таблице отмечены клетки, соответствующие транзитным состояниям, а кружочками с точкой - состояния, в которых оказывается автомат после завершения перехода. Горизонтальные линии со стрелкой определяют изменения входных сигналов, вертикальные сплошные линии - переходы автомата, а пунктирные линии - переходы обусловленные состязаниями.
Первый пример показывает как совершаются переходы в приведенной таблице. При этом автомат проходит последовательность состояний 000-001-101-111. Заметим, что в этой последовательности каждый переход в новое состояние совершается с изменением значения только одной внутренней переменой (одного элемента памяти), поэтому состязания отсутствуют.
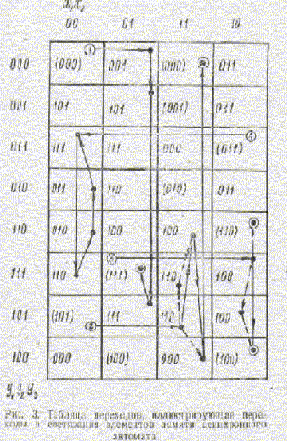
Во втором примере первый переход в последовательности состояний 101-110 выполняется с изменением значений двух внутренних переменных y2
и y3. Если время задерхки элементов памяти, соответствующим этим переменным, одинаково t32 = t33, то состязания отсутствуют и автомат проходит последовательность состояний 101 - 110-100-000.
Если же t32 < t33, то состязание выигрывает второй элемент памяти и из состояния 101 автомат попадает в состояние 111, совершая незапланированный переход. В этом случае автомат проходит последовательность состояний 101-111-110-100-000, заканчивающуюся устойчивым состоянием 000, в которое автомат должен попасть при отсутствии состязаний. Если t32
> t33, то автомат проходит последовательность состояний 101-100-000 и так же достигает заданного устойчивого состояния 000. Следовательно, в рассматриваемом случае имеют место некритические состязания. Пример показывает также, что некритические состяния огут изменять время, затрачиваемое автоматом на смену состояния, поскольку автомат может совершать различное число переходов в зависимости от соотношения между задежками.
В третьем примере (при отсутствии состязаний) автомат должен из состояния 111 перейти в состояние 100. Если же t32 > t33, то состязани выигрывает третий элемент памяти, и автомат вместо состония 100 оказывается в состоянии 110, которое является устойчивым. В этом случае имеют место критические состязания, поскольку автомат не достигает заплпнированного состояния 100.
Четвертый пример, приведенный в таблице, не связан с состязаниями элементов памяти. Он представляет собой иллюстрацию явления, встречающегося в асинхронных автоматах, которое называется генерацией. Это явление заключается в том, что автомат последовательно совершает переходы между транзитными состояниями, возвращаясь каждый раз в исходное состояние. Генерация прерывается при изменении входных сигналов. Однако при этом сосояние, в котором окажется автомат, зависит от того, с каким транзитным состоянием совпало изменение входного сигнала.
В заключение отметим, что одной из основных задач стадии структурного синтеза асинхронных автоматов является построение схемы без критических состязаний. Эта задача решается обычно на этапе кодирования состояний автомата.
Пред.Страница
След.Страница Раздел Содержание
