Дискретного времени
. Входные сигналы такого автомата подобны сигналам импульсного типа (рис. 1,а). При этом были приняты следующие ограничения:
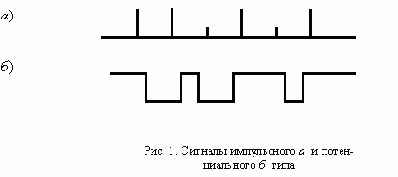
- сигналы могут поступать на вход автомата только в строго определенные моменты времени, задаваемые тактирующей последовательностью СИ с постоянным периодом Т;
- длительность входных сигналов t пренебрежимо мала (t ® 0);
- в промежутках между тактирующими сигналами на входе автомата сигнал отсутствует.
Модель автомата, построенная для токого сигнала, соответствует схемам, работающим с сигналами импульсного типа, элементы которых не имеют гальванической связи.
Входные сигналы асинхронного автомата подобны сигналам потенциального типа (рис. 1,б ). Такие сигналы должны обладать следующими свойствами:
- сигнал присктствует на входе автомата в каждый момент времени;
- длительность входного сигнала не ограничена и превышает некоторую минимальную величину t0;
- изменения входного сигнала могут происодить в произвоьные моменты времени.
Перечисленные свойства позволяют считать, что асинхронный автомат работает в непрерывном времени.
Ограничимся, так же как и для синхронного автомата, рассмотрением только двоичных входных сигналов. При этом модель асинхронного автомата может быть использована для описания работы схем, построенных из элементов потенциального типа. Допустим, что под действием входного сигнала pk синхронный автомат А переходит в состояние si. Согласно приведенным свойствам сигналов потенциального типа, pk присутствует на входе автомата и после того, как свершится переход, причем момент его окончания заранее не известен. Следовательно, выполнив такой переход, автомат должен оставаться в состоянии si до следующего изменения сигнала на входе. Описанную ситуацию можно обобщить в виде следующего определения. Если автомат совершает переход из некоторого состояния sj под действием сигнала pk в состояние si, т. е. j(sj, pk) = si, и остается под действием сигнала pk в этом же состоянии j(sj, pk) = si, то такое состояние называетсяустойчивым.
Приведенное определение позволяет нам уточнить понятие асинхронного автомата. Автомат, все состояния которого устойчивы, называется
